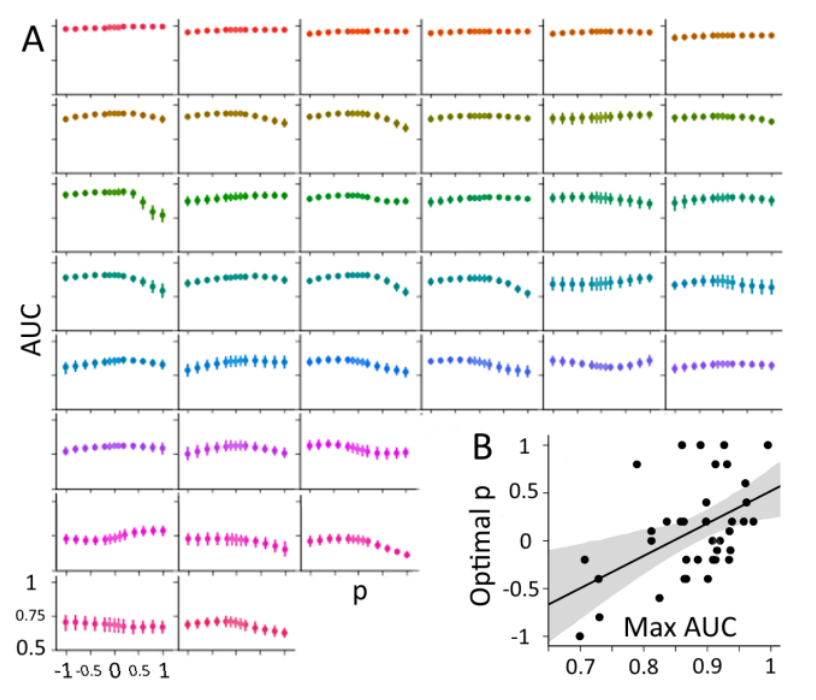
Estimating means of data points lying on the Riemannian manifold of symmetric positive-definite (SPD) matrices has proved of great utility in applications requiring interpolation, extrapolation, smoothing, signal detection and classification. The power means of SPD matrices with exponent p in the interval [-1, 1] interpolate in between the Harmonic mean (p = -1) and the Arithmetic mean (p = 1), while the Geometric (Cartan/Karcher) mean, which is the one currently employed in most applications, corresponds to their limit evaluated at 0. In this article we treat the problem of estimating power means along the continuum p(-1, 1) given noisy observed measurement. We provide a general fixed point algorithm (MPM) and we show that its convergence rate for p = ±0.5 deteriorates very little with the number and dimension of points given as input. Along the whole continuum, MPM is also robust with respect to the dispersion of the points on the manifold (noise), much more so than the gradient descent algorithm usually employed to estimate the geometric mean. Thus, MPM is an efficient algorithm for the whole family of power means, including the geometric mean, which by MPM can be approximated with a desired precision by interpolating two solutions obtained with a small ±p value. We also present an approximated version of the MPM algorithm with very low computational complexity for the special case p=±1⁄2. Finally, we show the appeal of power means through the classification of brain-computer interface event-related potentials data.