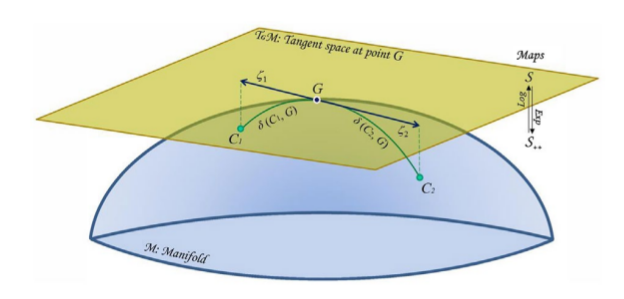
Despite its short history, the use of Riemannian geometry in brain-computer interface (BCI) decoding is currently attracting increasing attention, due to accumulating documentation of its simplicity, accuracy, robustness and transfer learning capabilities, including the winning score obtained in five recent international predictive modeling BCI data competitions. The Riemannian framework is sharp from a mathematical perspective, yet in practice it is simple, both algorithmically and computationally. This allows the conception of online decoding machines suiting real-world operation in adverse conditions. We provide here a review on the use of Riemannian geometry for BCI and a primer on the classification frameworks based on it. While the theoretical research on Riemannian geometry is technical, our aim here is to show the appeal of the framework on an intuitive geometrical ground. In particular, we provide a rationale for its robustness and transfer learning capabilities and we elucidate the link between a simple Riemannian classifier and a state-of-the-art spatial filtering approach. We conclude by reporting details on the construction of data points to be manipulated in the Riemannian framework in the context of BCI and by providing links to available open-source Matlab and Python code libraries for designing BCI decoders.